3.2.1 Perfect Competition
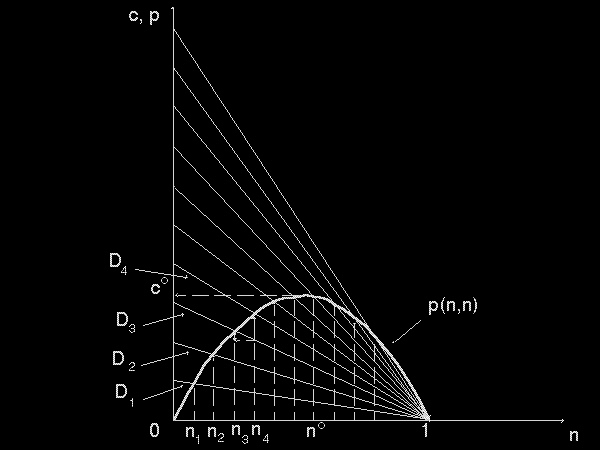
As we have noted earlier, network externalities arise out of the complementarity of different network pieces. Thus, they arise naturally in both one- and two-way networks, as well as in vertically-related markets. The value of good X increases as more of the complementary good Y is sold, and vice versa. Thus, more of Y is sold as more X is sold. It follows that the value of X increases as more of it is sold. This positive feedback loop seems explosive, and indeed it would be, except for the inherent downward slope of the demand curve. To understand this better, consider a fulfilled expectations formulation of network externalities as in Katz and Shapiro (1985), Economides (1993b, 1996a), and Economides and Himmelberg (1995). Let the willingness to pay for the nth unit of the good when ne units are expected to be sold be p(n;ne).14 This is a decreasing function of its first argument because the demand slopes downward. p(n; ne) increases in ne; this captures the network externalities effect. At a market equilibrium of the simple single-period world, expectations are fulfilled, n = ne, thus defining the fulfilled expectations demand p(n, n). Figure 5 shows the construction of a typical fulfilled expectations demand. Each curve Di, i = 1 ,..., 4, shows the willingness to pay for a varying quantity n, given an expectation of sales ne = ni. At n = ni, expectations are fulfilled and the point belongs to p(n, n) as p(ni, ni). Thus p(n, n) is constructed as a collection of points p(ni, ni).

Figure 5: Construction of the fulfilled expectations demand.
To avoid explosions and infinite sales, it is reasonable to impose lim(n-> infinity) p(n, n) = 0; it then follows that p(n, n) is decreasing for large n. Economides and Himmelberg (1995) show that the fulfilled expectations demand is increasing for small n if either one of three conditions hold: (i) the utility of every consumer in a network of zero size is zero, or (ii) there are immediate and large external benefits to network expansion for very small networks, or (iii) there is a significant density of high-willingness-to-pay consumers who are just indifferent on joining a network of approximately zero size. The first condition is straightforward and applies directly to all two-way networks. The other two conditions are a bit more subtle, but commonly observed in networks and vertically-related industries.
When the fulfilled expectations demand increases for small n, we say that the network exhibits a positive critical mass under perfect competition. This means that, if we imagine a constant marginal cost c decreasing parametrically, the network will start at a positive and significant size no (corresponding to marginal cost co). For each smaller marginal cost, c < co, there are three network sizes consistent with marginal cost pricing: a zero size network; an unstable network size at the first intersection of the horizontal through c with p(n, n); and the Pareto optimal stable network size at the largest intersection of the horizontal with p(n, n). The multiplicity of equilibria is a direct result of the coordination problem that arises naturally in the typical network externalities model. In such a setting, it is natural to assume that the Pareto optimal network size will result.15
In the presence of network externalities, it is evident that perfect competition is inefficient: The marginal social benefit of network expansion is larger than the benefit that accrues to a particular firm under perfect competition. Thus, perfect competition will provide a smaller network than is socially optimal, and for some relatively high marginal costs perfect competition will not provide the good while it is socially optimal to provide it.
One interesting question that remains virtually unanswered is how to decentralize the welfare maximizing solution in the presence of network externalities. Clearly, the welfare maximizing solution can be implemented through perfect price discrimination, but typically such discrimination is unfeasible. It remains to be seen to what extent mechanisms that allow for non-linear pricing and self-selection by consumers will come close to the first best.